Binary Decision Diagrams (BDDs)
| project staff | project description | project structure | publications
|
| Chair of Computer Architecture | |
| Rolf Drechsler, Prof. Dr. | |
| Wolfgang Günther, Dr. | |
For the verification of digital circuits binary decision diagrams (BDDs) were established in 1986. These don't only allow a compact and clear representation of boolean functions, but there are also efficient algorithms for manipulation. For example the AND of two functions can be achieved in time proportional to the product of both BDDs.
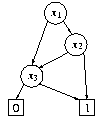
An example: for the boolean function f(x1,x2,x3) = x1 x2 + x3 the BDD is given by:
Optimizing the order of variables
The size of BDDs depends on the based order of the variables. Therefore their optimization is an important problem which has proved itself to be difficult (NP-hard). Due to this many heuristic methods for minimizing BDDs have been suggested up to now. To accelerate an exact method and also heuristics, lower bounds were used, which mainly were used in theoretical observations so far. Furthermore the heuristic minimization also analyses the best form of minimization depending on the previous setup-process.
Linerarly transformated BDDs (LTBDDs)
Since there are functions of exponential size under all orders of variables it is necessary to generalize BDDs so that the displaysize can be decreased but that there are still efficient BDDs for manipulation. Such an approach are linearly transformed BDDs (LTBDDs), which transform the inputvariables with the help of EXOR-links. Here an exponential difference in size could be shown, ther are good heuristics for minimizing display and synthesisoperations can still be processed efficiently.
Free BDDs (FBDDs)
Another generalization of BDDs are Free BDDs (FBDDs). Here an exponential difference is also possible in theory. However there aren’t very many efficient minimizationtechnics up till now. Here an exact method was presented and also a heuristic, which provides FBDDs which are smaller than the best known BDDs for the first time.
|
Wolfgang Günther, Dr., Rolf Drechsler, Prof. Dr. Linear Transformations and Exact Minimization of BDDs Great Lakes Symp. VLSI, 1998 |
|
Rolf Drechsler, Prof. Dr., Nicole Drechsler, Dr., Wolfgang Günther, Dr. Fast Exact Minimization of BDDs IEEE Design Automation Conference, 1998 |
|
Wolfgang Günther, Dr., Rolf Drechsler, Prof. Dr. BDD Minimization by Linear Transformations Advanced Computer Systems, 1998 |
|
Wolfgang Günther, Dr., Rolf Drechsler, Prof. Dr. Minimization of Free BDDs ASP Design Automation Conf., 1999 |
|
Wolfgang Günther, Dr., Rolf Drechsler, Prof. Dr. Minimization of BDDs using Linear Transformations based on Evolutionary Techniques IEEE International Symposium on Circuits and Systems, 1999 |
|
Rolf Drechsler, Prof. Dr., Wolfgang Günther, Dr. Using Lower Bounds During Dynamic BDD Minimization IEEE Design Automation Conference, 1999 |
|
Wolfgang Günther, Dr., Rolf Drechsler, Prof. Dr. Efficient Manipulation Algorithms for Linearly Transformed BDDs International Conference on Computer Aided Design, 1999 |
|
Rolf Drechsler, Prof. Dr., Wolfgang Günther, Dr. History-based Dynamic Minimization during BDD Construction X IFIP International Conference on VLSI, 1999 |
|
Rolf Drechsler, Prof. Dr., Wolfgang Günther, Dr. Optimization of Sequential Verification by History-Based Dynamic Minimization of BDDs IEEE International Symposium on Circuits and Systems, 2000 |
|
Wolfgang Günther, Dr. Minimization of Free BDDs using Evolutionary Techniques Int'l Workshop on Logic Synthesis, 2000 |
|
Wolfgang Günther, Dr., Rolf Drechsler, Prof. Dr. On the Computational Power of Linearly Transformed BDDs Information Processing Letters, 75(3):119-125, 2000 |
