timemachine
| project staff | description | benchmarks | publications
|
| Chair of Computer Architecture | |
| Karina Gitina, Dipl.-Inf. | developer |
| Christian Miller, Dipl.-Inf. | developer / contact |
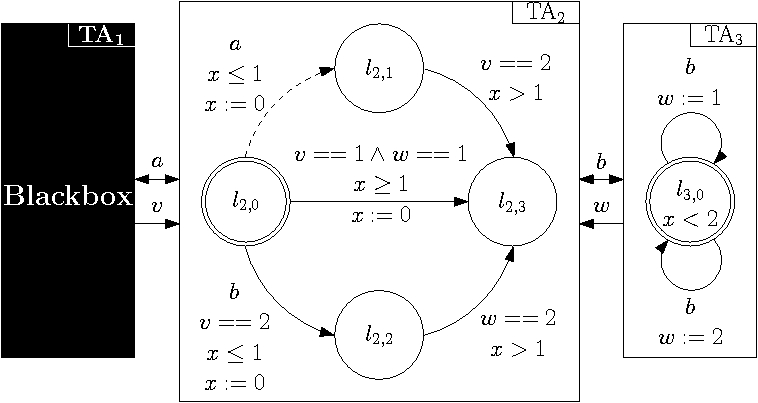
Timemachine is a bounded model checker for incomplete networks of timed automata to prove unrealizability of an invariant. This tool supports multiple prevalent communication models, and allows the user to select several subautomata of the network as blackboxes. Furthermore, it can be specified how the unknown behavior of each blackbox output is modeled (abstraction technique based on fixed transitions or based on universal quantification). Timemachine uses Yices and MathSAT as back-end SMT solvers. If a more precise modeling based on universal quantification is required, the resulting quantified SMT formulas are solved using either LIRA or LinAIGs. As input, timemachine accepts networks of timed automata given in the standard UPPAAL file format, and makes use of the opensource parser library UTAP. As blackbox outputs we consider synchronization (channels), broadcast channels, bounded integer variables and clocks which are reset in blackboxed subautomata.
Fischer Protocol: For several concurrent processes, the Fischer Protocol guarantees mutual exclusion to enter a critical region. In the original design one integer variable to determine which process may enter the critical region is used. In contrast, we simulate this variable with an additional subautomaton so that the overall communication in the network relies on the synchronization model. We inserted an error into each process by changing a clock constraint consisting of a strict inequality to a non-strict inequality and tested whether a network state can be reached where the first n processes are in the critical section at the same time with the remaining processes modeled as blackboxes.
Processes With Arbiters: This design is a mutual exclusion protocol, where each process has its own arbiter. The processes are interacting via synchronization with its arbiters and a counter decides via an bounded integer variable which process may proceed next. We considered two blackbox scenarios for this benchmark. First, we model several processes as blackboxes and prove that the remaining n implemented processes can reach a safe location at the same time. In our second scenario, we insert an error into each arbiter allowing their process to proceed for each value of the bounded integer variable, which is set by the counter subautomaton. Using linAIGs as solver for quantified SMT formulas, we are able to model the counter as a blackbox and prove that there is a path into the state described above for all possible values of the bounded integer variable.
FlexRay Protocol: This network of timed automata is a simple version of the physical layer of the FlexRay Protocol. Here, the strobing unit, the sending module and the voting module, which are interacting via several regular channels, broadcast channels and bounded integer variables with the implemented system, are blackboxed. Furthermore one clock which occurs in guards of transitions in the implemented automata, is reset in the blackboxed voting module. An error is inserted into the receiver leading to an error location denoting a failure of the transmission. The error path depends on the bounded integer variable which is assigned to in the blackboxed strobing unit, and on the blackboxed clock of the voter. Thus, these variables have to be universally quantified to prove unrealizability of the property that states, that the error location of the receiver can never be reached. The remaining blackbox outputs are modeled using fixed transitions.
Gear Production Stack: This benchmark models a sequence of n production cells for gears. Each cell communicates its completion via synchronization and one bounded integer variable to the next one, which then can continue the production process. A controlling module initiates the production process and checks whether one gear is produced on time, otherwise it enters an error location denoting a timeout of the production. In this design, the time setting of the controller is erroneous, that is, the production will always terminate too late. A further error in the controlling unit forces the production stack to skip the first station, which is modeled as a blackbox. To prove unrealizability of the property that the production completes in time, it is necessary to use universal quantification for bounded integer variable and the clock of the blackboxed production cell, since this clock occurs in guards of transitions of the implemented system.
|
Christian Miller, Karina Gitina, Christoph Scholl, Bernd Becker Bounded Model Checking of Incomplete Networks of Timed Automata Microprocessor Test and Verification Workshop (MTV), 2010 |
|
Christian Miller, Christoph Scholl, Bernd Becker Verifying Incomplete Networks of Timed Automata GI/ITG/GMM Workshop Methoden und Beschreibungssprachen zur Modellierung und Verifikation von Schaltungen und Systemen (MBMV), 2011 |
