Binary Decision Diagrams (BDDs)

| Beteiligte Mitarbeiter | Projektbeschreibung | Struktur des Projekts | Publikationen |

Beteiligte Mitarbeiter
Lehrstuhl für Rechnerarchitektur
Rolf Drechsler, Prof. Dr.
Wolfgang Günther, Dr.

Zur Verifikation digitaler Schaltungen wurden 1986 Binary Decision Diagrams (BDDs) eingeführt. Diese erlauben nicht nur eine kompakte und eindeutige Repräsentation von Booleschen Schaltungen, sondern es existieren auch effiziente Algorithmen zur Manipulation. So kann beispielsweise das UND zweier Funktionen in Zeit proportional zum Produkt der beiden BDDs ausgeführt werden.
Ein Beispiel: für die Boolesche Funktion f(x1,x2,x3) = x1 x2 + x3 ist der BDD gegeben durch:

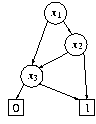
Optimierung der Variablenordnung

Die Größe von BDDs hängt stark von der zugrundeliegenden Ordnung der Variablen ab. Deshalb ist deren Optimierung ein wichtiges Problem, das allerdings bewiesenermaßen schwierig ist (NP-hart). Deshalb wurden bisher viele heuristische Verfahren zur Minimierung von BDDs vorgeschlagen. Zur Beschleunigung sowohl eines exakten Verfahrens als auch von Heuristiken wurden untere Schranken verwendet, welche bisher hauptsächlich in theoretischen Betrachtungen eingesetzt wurden. Weiterhin wurde bei der heuristischen Minimierung auch untersucht, wie in Abhängigkeit von dem bisherigen Aufbauprozeß am besten minimiert werden sollte.

Linear Transformierte BDDs (LTBDDs)

Da es jedoch Funktionen gibt, die unter allen Variablenordnungen exponentielle Größe haben, sind Verallgemeinerungen von BDDs vonnöten, die zwar die Darstellungsgröße reduzieren können, es aber auch weiterhin effiziente Algorithmen zur Manipulation gibt. Ein solcher Ansatz sind linear transformierte BDDs (LTBDDs), welche die Eingabevariablen mit Hilfe von EXOR-Verknüpfungen transformieren. Hier konnte ein exponentieller Unterschied in der Größe gezeigt werden, es gibt gute Heuristiken zur Minimierung der Darstellung und Syntheseoperationen können weiterhin effizient ausgeführt werden.

Freie BDDs (FBDDs)

Eine weitere Verallgemeinerung von BDDs sind Freie BDDs (FBDDs). Auch hier ist in der Theorie ein exponentieller Unterschied möglich. Bisher gibt es allerdings noch kaum gute Minimierungstechniken. Hier wurde sowohl ein exaktes Verfahren vorgestellt als auch eine Heuristik, die zum ersten Mal FBDDs liefert, die kleiner sind als die besten bekannten BDDs.

Wolfgang Günther, Dr., Rolf Drechsler, Prof. Dr. Linear Transformations and Exact Minimization of BDDs Great Lakes Symp. VLSI, 1998

Rolf Drechsler, Prof. Dr., Nicole Drechsler, Dr., Wolfgang Günther, Dr. Fast Exact Minimization of BDDs IEEE Design Automation Conference, 1998

Wolfgang Günther, Dr., Rolf Drechsler, Prof. Dr. BDD Minimization by Linear Transformations Advanced Computer Systems, 1998

Wolfgang Günther, Dr., Rolf Drechsler, Prof. Dr. Minimization of Free BDDs ASP Design Automation Conf., 1999

Wolfgang Günther, Dr., Rolf Drechsler, Prof. Dr. Minimization of BDDs using Linear Transformations based on Evolutionary Techniques IEEE International Symposium on Circuits and Systems, 1999

Rolf Drechsler, Prof. Dr., Wolfgang Günther, Dr. Using Lower Bounds During Dynamic BDD Minimization IEEE Design Automation Conference, 1999

Wolfgang Günther, Dr., Rolf Drechsler, Prof. Dr. Efficient Manipulation Algorithms for Linearly Transformed BDDs International Conference on Computer Aided Design, 1999

Rolf Drechsler, Prof. Dr., Wolfgang Günther, Dr. History-based Dynamic Minimization during BDD Construction X IFIP International Conference on VLSI, 1999

Rolf Drechsler, Prof. Dr., Wolfgang Günther, Dr. Optimization of Sequential Verification by History-Based Dynamic Minimization of BDDs IEEE International Symposium on Circuits and Systems, 2000

Wolfgang Günther, Dr. Minimization of Free BDDs using Evolutionary Techniques Int'l Workshop on Logic Synthesis, 2000

Wolfgang Günther, Dr., Rolf Drechsler, Prof. Dr. On the Computational Power of Linearly Transformed BDDs Information Processing Letters, 75(3):119-125, 2000